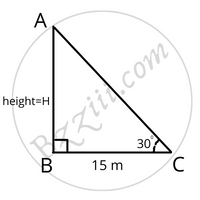
A Tower Stands Vertically on the Ground. From a Point on the Ground, Which is 15 m away From the Foot of the Tower, the Angle of Elevation of the Top of the Tower is Found to be 30°. Find the Height of the Tower - Bzziii

By admin -
A tower stands vertically on the ground. From a point on the ground, which is 15 m away from the foot of the tower, the angle of elevation of the top of the tower is found to be 30°. Find the height of the tower.

(a) `5\sqrt{3}` m
(b) `15\sqrt{3}` m
(c) 15 m
(d) `\frac{5}{\sqrt{3}}` m





(b) `15\sqrt{3}` m



Option (b)`15/\sqrt{3}` is the correct answer.

Let, the height of the tower be H meter.

So, AB = H meter

Distance of the point from the foot of the tower = 15m

Hence, CB = 15 m

Angle of elevation = `30^0`

∠ACB = `30^0`

Since, the tower is vertical to ground,

So, ∠ABC = `30^0`

Now,

tan C = `"side opposite to angle C"/"side adjacent to angle C"`

tan C = `"AB"/"CB"`

tan `30^0` = `"AB"/"CB"`

⇒ `1/\sqrt{3}` = `"AB"/"CB"`

⇒ `1/\sqrt{3}` = `"H"/"15"`

⇒ 15 = H`\sqrt{3}`

⇒ `15/\sqrt{3}` = H

∴ H = `15/\sqrt{3}` 

Comments

Post a Comment

Popular posts from this blog

Explain the Role of ‘Justice Party’ in Boycotting of Council Elections | bzziii.com

By admin -
answer source Question Read the source given below and answer the questions that follows: Source : The Movement in the Towns The movement started with middle-class participation in the cities. Thousands of students left government-controlled schools and colleges, headmasters and teachers resigned, and lawyers gave up their legal practices. The council elections were boycotted in most provinces except Madras, where the Justice Party, the party of the non-Brahmans, felt that entering the council was one way of gaining some power–something that usually only Brahmans had access to. The effects of non-cooperation on the economic front were more dramatic. Foreign goods were boycotted, liquor shops picketed, and foreign cloth burnt in huge bonfires. The import of foreign cloth halved between 1921 and 1922, its value dropping from Rs. 102 crore to Rs. 57 crore. In many places merchants and traders refused to trade in foreign goods or finance foreign trade. As the boycott movement spread...
Read more

Who do you think is the ‘well-dressed customer’ at the shop?

By admin -
Read the following passage. At the shop there was a well-dressed customer. He bent down and asked the little girl, “What kind of a miracle does your brother need? “I don’t know,” she replied with her eyes welling up. “He’s really sick and Mummy says he needs an operation. But my Daddy can’t pay for it, so I have brought my savings.” “How much do you have?” asked the man. “One dollar and eleven cents, but I can try and get some more,” she answered barely audible. Answer the following questions. 1) Who do you think is the ‘well-dressed customer’ at the shop? 2) What did the well-dressed man ask the little girl? 3) “He’s really sick.” Who does title word ‘he’ refer to here ? What is he to Tess? 4) What did he need urgently? 5) How much money did the little girl have with her? SOLUTION 1. I think the well-dressed customer at the shop is Dr. Carlton Armstrong. 2. The well-dressed man asked the little girl what kind of a miracle her brother needed. 3. The word ‘he’ refers to A...
Read more

A Trading Firm’s Average Inventory Is Rs 20,000 (Cost). If The Inventory Turnover Ratio Is 8 Times And The Firm Sells Goods At A Profit Of 20% On Sale, Ascertain the Profit of the firm.

By admin -
Image
A trading firm’s average inventory is Rs 20,000 (cost). If the inventory turnover ratio is 8 times and the firm sells goods at a profit of 20% on sale, ascertain the profit of the firm. SOLUTION Inventory Turn Over Ratio  Or,8  Or, Cost of Revenue from Operations  = 20,000 ❌ 8 = 1,60,000 Let Sales Price be Rs. 100 ∴ Profit is Rs.20 Hence, the Cost of Revenue from Operations  = Rs. 100 - Rs. 20 = Rs. 80 If the Cost of Revenue  from Operations   = Rs. 100 - Rs. 20  = Rs. 80 If the Cost of Revenue  from Operations is Rs. 80, then Revenue from Operations = 100 If the Cost of Revenue  from Operations is Rs. 1, then Revenue from Operations = ` `\frac{100}{8}` ` If the Cost of Revenue  from Operations is Rs. 1,60,000 then, Revenue from Operations = ` `\frac{100}{8}\times1,60,000` ` = 2,00,000 Now, Profit = Net Revenue from Operations - Cost of Revenue  from Operations   = 2,00,000 - 1,60,000 = 40,000 Alternative Method: Stoc...
Read more